СибГУТИ Контрольная работа Вариант 18 Математика (часть 3) скачать бесплатно
Дистанционное обучение
Направление «Информатика и вычислительная техника»
Профиль «Программное обеспечение средств вычислительной техники и автоматизированных систем»
Дисциплина «Математика» Часть 3.
Вариант № 8
1. Найти область сходимости степенного ряда
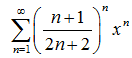
Решение.
Радиус сходимости степенного ряда можно найти по формуле Коши: .
Т.к. , то
Итак, радиус сходимости ряда . Определим интервал сходимости данного степенного ряда:
Т.о., – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.
Пусть . Подставим в заданный степенной ряд и получим знакочередующийся ряд
Для членов полученного ряда выполняется условие:
В соответствии с признаком Лейбница данный ряд расходится и не принадлежит области сходимости степенного ряда.
Пусть . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами:
Для членов полученного ряда выполняется условие:
Следовательно, ряд расходится не выполняется необходимый признак сходимости и не принадлежит области сходимости степенного ряда. Итак, областью сходимости данного степенного ряда является промежуток .
Ответ: .
2. Разложить функцию в ряд Фурье на данном отрезке (период Т)
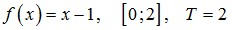
Решение.
Разложение функции на интервале в ряд Фурье имеет вид:
, где
Находим коэффициенты ряда Фурье:
Разложение функции в ряд Фурье примет вид:
Ответ: .
3. Начертить область на комплексной плоскости по данным условиям:
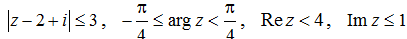
Решение.
Условие определяет область внутри круга радиуса 3 центром в точке (2;-1).
Условие определяет внутренность угла, образованного лучами, исходящими из точки 0, под углами и к положительному направлению действительной оси.
Условие определяет левую полуплоскость от вертикальной прямой .
Наконец, условие определяет нижнюю полуплоскость от горизонтальной прямой .
Учитывая все данные неравенства, получим область, заштрихованную на последнем чертеже.
4. Вычислить интеграл по дуге от точки до точки
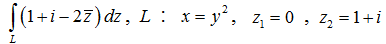
Решение.
Заметим, что
Тогда
Учитывая, что интегрирование ведется по линии , получим
Ответ: .
Направление «Информатика и вычислительная техника»
Профиль «Программное обеспечение средств вычислительной техники и автоматизированных систем»
Дисциплина «Математика» Часть 3.
Вариант № 8
1. Найти область сходимости степенного ряда
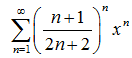
Решение.
Радиус сходимости степенного ряда можно найти по формуле Коши: .
Т.к. , то
Итак, радиус сходимости ряда . Определим интервал сходимости данного степенного ряда:
Т.о., – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.
Пусть . Подставим в заданный степенной ряд и получим знакочередующийся ряд
Для членов полученного ряда выполняется условие:
В соответствии с признаком Лейбница данный ряд расходится и не принадлежит области сходимости степенного ряда.
Пусть . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами:
Для членов полученного ряда выполняется условие:
Следовательно, ряд расходится не выполняется необходимый признак сходимости и не принадлежит области сходимости степенного ряда. Итак, областью сходимости данного степенного ряда является промежуток .
Ответ: .
2. Разложить функцию в ряд Фурье на данном отрезке (период Т)
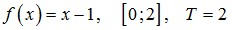
Решение.
Разложение функции на интервале в ряд Фурье имеет вид:
, где
Находим коэффициенты ряда Фурье:
Разложение функции в ряд Фурье примет вид:
Ответ: .
3. Начертить область на комплексной плоскости по данным условиям:
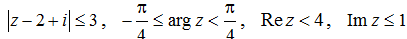
Решение.
Условие определяет область внутри круга радиуса 3 центром в точке (2;-1).
Условие определяет внутренность угла, образованного лучами, исходящими из точки 0, под углами и к положительному направлению действительной оси.
Условие определяет левую полуплоскость от вертикальной прямой .
Наконец, условие определяет нижнюю полуплоскость от горизонтальной прямой .
Учитывая все данные неравенства, получим область, заштрихованную на последнем чертеже.
4. Вычислить интеграл по дуге от точки до точки
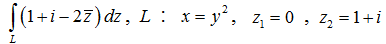
Решение.
Заметим, что
Тогда
Учитывая, что интегрирование ведется по линии , получим
Ответ: .







