СибГУТИ Лабораторная 3 Вариант 8 Алгоритмы и вычислительные методы оптимизации скачать бесплатно
Задание
Написать программу, находящую решение задачи нелинейного программирования методом Эрроу-Гурвица с точностью 0.0001.
Вариант выбирается по последней цифре пароля.
Вариант 8
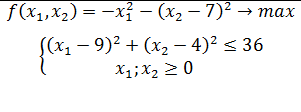
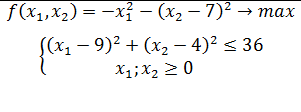
Выбранный язык программирования C#
Градиентные методы и метод Эрроу-Гурвица
Используя градиентные методы можно найти решение любой задачи нелинейного программирования. В общем случае применение таких методов позволяет найти локальный экстремум. Поэтому градиентными методами лучше решать задачи выпуклого программирования, в которых локальный экстремум является глобальным.
Процесс нахождения решения градиентными методами заключается в том, что начиная с некоторой точки , осуществляется последовательный переход к другим точкам до тех пор, пока градиент в некоторой точке не станет равным 0 или пока не будет выполняться условие , где – достаточно малое положительное число.
Градиентные методы делятся на две группы. К первой группе относятся методы, в которых исследуемые точки не выходят за границы области допустимых решений. Наиболее известный из таких методов – метод Франка-Вулфа. Ко второй группе относятся методы, в которых исследуемые точки могут как принадлежать, так и не принадлежать ОДР. Наиболее известные из таких методов – метод штрафных функций, Эрроу-Гурвица.
В методе Эрроу-Гурвица на очередном шаге коэффициенты вычисляются по формуле:
,
где – последнее предыдущее ненулевое значение, если оно было.
В качестве начальных значений берут произвольные неотрицательные числа.
Исходный текст программы
...
Результаты работы программы
Ishodnie dannie:
f(x1,x2) = - x1^2 - (x2 - 7)^2 -> max
(x1 - 9)^2 + (x2 - 4)^2 <= 36
x1;x2 >= 0
Vozmem lyuboe dopustimoe reshenie sistemi ogranicheniy v kachestve nachalnogo priblizheniya:
x1 = 6, x2 = 8
f(6,8) = -37
V kachestve nachalnogo shaga vichisleniy viberem 'lambda' = 0,1; 'alpha' = 0
Vvedem oboznachenie:
g(x1,x2) = 36 - (x1 - 9)^2 -(x2 - 4)^2
Opredelim chastnie proizvodnie:
fx1 = -2 * x1
fx2 = -2 * x2 + 14
gx1 = -2 * x1 + 18
gx2 = -2 * x2 + 8
Iteration 1:
--------------------
'Alpha' = 0,000
x1 = 4,800
x2 = 7,800
Polichili novuyuy tochku x1 = (4,800; 7,800)
g(x1) = 3,920 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x1) = -23,680
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x1) - f(x0)| = 13,32000
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 2:
--------------------
'Alpha' = 0,000
x1 = 3,840
x2 = 7,640
Polichili novuyuy tochku x2 = (3,840; 7,640)
g(x2) = -3,875 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 3:
--------------------
'Alpha' = 0,388
x1 = 3,472
x2 = 7,230
Polichili novuyuy tochku x3 = (3,472; 7,230)
g(x3) = -4,992 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 4:
--------------------
'Alpha' = 0,887
x1 = 3,758
x2 = 6,611
Polichili novuyuy tochku x4 = (3,758; 6,611)
g(x4) = 1,702 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x4) = -14,273
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x4) - f(x1)| = 9,40705
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 5:
--------------------
'Alpha' = 0,000
x1 = 3,006
x2 = 6,689
Polichili novuyuy tochku x5 = (3,006; 6,689)
g(x5) = -7,154 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 6:
--------------------
'Alpha' = 0,715
x1 = 3,263
x2 = 6,366
Polichili novuyuy tochku x6 = (3,263; 6,366)
g(x6) = -2,516 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 7:
--------------------
'Alpha' = 0,967
x1 = 3,720
x2 = 6,035
Polichili novuyuy tochku x7 = (3,720; 6,035)
g(x7) = 3,977 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x7) = -14,768
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x7) - f(x4)| = 0,49483
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 8:
--------------------
'Alpha' = 0,000
x1 = 2,976
x2 = 6,228
Polichili novuyuy tochku x8 = (2,976; 6,228)
g(x8) = -5,255 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 9:
--------------------
'Alpha' = 0,526
x1 = 3,014
x2 = 6,148
Polichili novuyuy tochku x9 = (3,014; 6,148)
g(x9) = -4,449 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 10:
--------------------
'Alpha' = 0,970
x1 = 3,573
x2 = 5,902
Polichili novuyuy tochku x10 = (3,573; 5,902)
g(x10) = 2,931 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x10) = -13,972
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x10) - f(x7)| = 0,79545
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 11:
--------------------
'Alpha' = 0,000
x1 = 2,858
x2 = 6,121
Polichili novuyuy tochku x11 = (2,858; 6,121)
g(x11) = -6,220 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 12:
--------------------
'Alpha' = 0,622
x1 = 3,051
x2 = 6,033
Polichili novuyuy tochku x12 = (3,051; 6,033)
g(x12) = -3,528 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 13:
--------------------
'Alpha' = 0,975
x1 = 3,600
x2 = 5,830
Polichili novuyuy tochku x13 = (3,600; 5,830)
g(x13) = 3,495 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x13) = -14,332
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x13) - f(x10)| = 0,35925
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 14:
--------------------
'Alpha' = 0,000
x1 = 2,880
x2 = 6,064
Polichili novuyuy tochku x14 = (2,880; 6,064)
g(x14) = -5,711 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 15:
--------------------
'Alpha' = 0,571
x1 = 3,003
x2 = 6,016
Polichili novuyuy tochku x15 = (3,003; 6,016)
g(x15) = -4,024 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 16:
--------------------
'Alpha' = 0,973
x1 = 3,570
x2 = 5,820
Polichili novuyuy tochku x16 = (3,570; 5,820)
g(x16) = 3,204 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x16) = -14,138
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x16) - f(x13)| = 0,19374
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 17:
--------------------
'Alpha' = 0,000
x1 = 2,856
x2 = 6,056
Polichili novuyuy tochku x17 = (2,856; 6,056)
g(x17) = -5,975 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 18:
--------------------
'Alpha' = 0,598
x1 = 3,019
x2 = 5,999
Polichili novuyuy tochku x18 = (3,019; 5,999)
g(x18) = -3,768 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 19:
--------------------
'Alpha' = 0,974
x1 = 3,581
x2 = 5,810
Polichili novuyuy tochku x19 = (3,581; 5,810)
g(x19) = 3,356 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x19) = -14,238
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x19) - f(x16)| = 0,10039
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 20:
--------------------
'Alpha' = 0,000
x1 = 2,865
x2 = 6,048
Polichili novuyuy tochku x20 = (2,865; 6,048)
g(x20) = -5,837 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 21:
--------------------
'Alpha' = 0,584
x1 = 3,008
x2 = 5,999
Polichili novuyuy tochku x21 = (3,008; 5,999)
g(x21) = -3,902 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 22:
--------------------
'Alpha' = 0,974
x1 = 3,573
x2 = 5,810
Polichili novuyuy tochku x22 = (3,573; 5,810)
g(x22) = 3,277 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x22) = -14,186
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x22) - f(x19)| = 0,05245
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 23:
--------------------
'Alpha' = 0,000
x1 = 2,859
x2 = 6,048
Polichili novuyuy tochku x23 = (2,859; 6,048)
g(x23) = -5,909 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 24:
--------------------
'Alpha' = 0,591
x1 = 3,013
x2 = 5,996
Polichili novuyuy tochku x24 = (3,013; 5,996)
g(x24) = -3,832 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 25:
--------------------
'Alpha' = 0,974
x1 = 3,577
x2 = 5,808
Polichili novuyuy tochku x25 = (3,577; 5,808)
g(x25) = 3,318 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x25) = -14,213
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x25) - f(x22)| = 0,02735
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 26:
--------------------
'Alpha' = 0,000
x1 = 2,861
x2 = 6,047
Polichili novuyuy tochku x26 = (2,861; 6,047)
g(x26) = -5,871 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 27:
--------------------
'Alpha' = 0,587
x1 = 3,010
x2 = 5,997
Polichili novuyuy tochku x27 = (3,010; 5,997)
g(x27) = -3,869 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 28:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,809
Polichili novuyuy tochku x28 = (3,575; 5,809)
g(x28) = 3,297 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x28) = -14,199
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x28) - f(x25)| = 0,01427
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 29:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x29 = (2,860; 6,047)
g(x29) = -5,891 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 30:
--------------------
'Alpha' = 0,589
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x30 = (3,011; 5,996)
g(x30) = -3,850 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 31:
--------------------
'Alpha' = 0,974
x1 = 3,576
x2 = 5,808
Polichili novuyuy tochku x31 = (3,576; 5,808)
g(x31) = 3,308 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x31) = -14,206
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x31) - f(x28)| = 0,00745
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 32:
--------------------
'Alpha' = 0,000
x1 = 2,861
x2 = 6,047
Polichili novuyuy tochku x32 = (2,861; 6,047)
g(x32) = -5,881 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 33:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,997
Polichili novuyuy tochku x33 = (3,011; 5,997)
g(x33) = -3,860 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 34:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x34 = (3,575; 5,808)
g(x34) = 3,302 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x34) = -14,202
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x34) - f(x31)| = 0,00388
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 35:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x35 = (2,860; 6,047)
g(x35) = -5,886 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 36:
--------------------
'Alpha' = 0,589
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x36 = (3,011; 5,996)
g(x36) = -3,854 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 37:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x37 = (3,575; 5,808)
g(x37) = 3,305 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x37) = -14,204
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x37) - f(x34)| = 0,00203
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 38:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x38 = (2,860; 6,047)
g(x38) = -5,883 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 39:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x39 = (3,011; 5,996)
g(x39) = -3,857 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 40:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x40 = (3,575; 5,808)
g(x40) = 3,303 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x40) = -14,203
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x40) - f(x37)| = 0,00106
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 41:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x41 = (2,860; 6,047)
g(x41) = -5,885 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 42:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x42 = (3,011; 5,996)
g(x42) = -3,856 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 43:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x43 = (3,575; 5,808)
g(x43) = 3,304 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x43) = -14,204
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x43) - f(x40)| = 0,00055
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 44:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x44 = (2,860; 6,047)
g(x44) = -5,884 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 45:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x45 = (3,011; 5,996)
g(x45) = -3,856 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 46:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x46 = (3,575; 5,808)
g(x46) = 3,304 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x46) = -14,204
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x46) - f(x43)| = 0,00029
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 47:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x47 = (2,860; 6,047)
g(x47) = -5,884 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 48:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x48 = (3,011; 5,996)
g(x48) = -3,856 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 49:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x49 = (3,575; 5,808)
g(x49) = 3,304 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x49) = -14,204
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x49) - f(x46)| = 0,00015
Tochnost menshe chem 0,0001 ne dostignuta. Prodoljaem iteracionniy process.
Iteration 50:
--------------------
'Alpha' = 0,000
x1 = 2,860
x2 = 6,047
Polichili novuyuy tochku x50 = (2,860; 6,047)
g(x50) = -5,884 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 51:
--------------------
'Alpha' = 0,588
x1 = 3,011
x2 = 5,996
Polichili novuyuy tochku x51 = (3,011; 5,996)
g(x51) = -3,856 < 0
Naidennaya tochka ne prinadlejit oblasti dopustimih resheniy.
Iteration 52:
--------------------
'Alpha' = 0,974
x1 = 3,575
x2 = 5,808
Polichili novuyuy tochku x52 = (3,575; 5,808)
g(x52) = 3,304 > 0
Naidennaya tochka prinadlejit oblasti dopustimih resheniy.
f(x52) = -14,204
Proverim dostizhenie trebuemoi tochnosti (sravnivaem so znacheniem funkcii v tochke, kotoraya posldney popadala v oblast):
|f(x52) - f(x49)| = 0,00008
Tochnost menshe chem 0,0001 dostignuta!
Rezultati:
Nomer iteracii = 52.
Tochka x52 = (3,575; 5,808)
Окно работы программы







